Sergio Pezzini & Uli Zeitler, HFML Nijmegen

Using high magnetic-magnetic fields, the Bloch states in two-dimensional graphene superlattices can be influenced in a way that adding fractions of flux quanta into a superlattice unit cell lead to high temperature quantum oscillations in its resistance. This phenomenon can be explained by the recurrence of straight trajectories of the Bloch states whenever a fraction p/q of flux quanta threads through a unit cell yielding a self-similar fractal electronic spectra around this points which can then be interpreted as an effective zero magnetics field.

Researchers from the University of Manchester have now extended the parameter range of this so-called Brown-Zack oscillations [1,2] to higher electron concentrations and higher magnetic fields (30T) available at HFML Nijmegen. This has allowed the observation of a fractal pattern in the conductance originating from high-order magnetic Bloch states (p > 1) which agrees well with band-structure calculations Although predicted more than half century ago, it was only possible now to observe and model these intriguing electronic states convincingly.

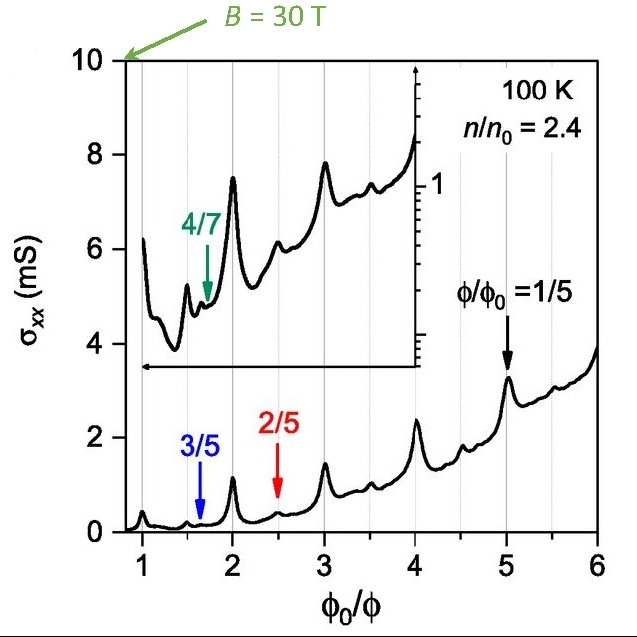
Figure: High-order magnetic Bloch states in a graphene superlattice: The conductivity sxx as a function of the inverse magnetic field expressed in units of f0/f up to 30 T (left end). The recurring maxima at of f/f0 = p/q can be interpreted as fractal Bloch states in an effective zero magnetic field.
In order to emphasize weaker features, the inset shows the same data on a logarithmic vertical scale with the same horizontal axes.

[1] E. Brown, Bloch electrons in a uniform magnetic field, Phys. Rev. 133, A1038 (1964); J. Zak, Magnetic translation group. Phys. Rev. 134, A1602 (1964).[2] R. Krishna Kumar et al., High-temperature quantum oscillations caused by recurring Bloch states in graphene superlattices. Science 357, 181 (2017).

High-order fractal states in graphene superlattices

R. Krishna Kumar, A. Mishchenko, X. Chen, S. Pezzini, G.H. Auton, L.A. Ponomarenko, U. Zeitler, L. Eaves, V. I. Fal’ko and A. K. Geim, Proc. Natl. Acad. Sci. USA 115, 5139 (2018).